Alkusanat
Otetaan muutama peruste heti alkuunsa.
- Avaruuteen on helppo päästä. Siellä pysyminen on vaikeaa.
- Kiertoradalle pääsyyn on mentävä suurella nopeudella sivusuunnassa
- Kiertoratamuutoksissa mielekäs yksikkö on joko km/s tai m/s.
- Ap(sis) on termi joka tarkoittaa kahta ääripistettä-
- Apoapsis planeetasta riippumaton radan korkein korkeus
- Periapsis on planeetasta riippumaton radan matalin korkeus
- Planeetoille ja taivaankappaleille on oma jälkiliitteensä
- -gee jälkiliite tarkoittaa Maata (Perigee, Apogee).
- -helion jälkiliite tarkoittaa aurinkoa (Aphelion, perihelion)
Jokainen objekti avaruudessa on jollakin kiertoradalla, poislukien elektromagneettinen säteily ja sen partikkelit. Kaikki liikehdintä aurinkokunnassa ja sen planeetta järjestelmien välillä tapahtuu aina kiertoradoilla, jos haluaa liikkua paikasta toiseen.
Ratojen laadut
Kiinteät radat ja ratojen muodot
Ratamatematiikka on kiistattoman vaikeaa ja viljelee terminologiaa joka johtaa mielellään asiasta kiinnostunutta maallikkoa harhaan. Alan kirjallisuudessa viljellään kolsolti termejä eksentrisyydestä, baryosenteristä, inklinaatioista, rataprekessiosta, ja n-body matematiikasta.
Ylläolevat ovat tarpeellisia tietoja, mutta niitä on pakko yksinkertaistaa. Tämän artikkelin tavoite on esitellä muutamia perusmuotoja radoista ja niiden mekaniikasta. Mennään mielekkyys edellä.
Suborbitaaliset radat
Kun raketti lähtee maan pinnalta, raketin sanotaan olevan suborbitaalisella radalla. Toisin sanoen, perigee ei ole vielä maatason yläpuolella- Radat kiertävät massakeskipistettä, joka ei ole sama kuin planeetan pinta. Kun rata saavuttaa positiivisen perigeen, radan alin piste on riittävän korkealla, on raketti päässyt pois suborbitaaliselta radalta ja päässyt kiertoradalle.
Ympyrärata
Yksinkertaisin rata jota voidaan ajatella on ympyrärata massakeskipisteen ympäri. Tämä tarkoittaa päiväntasaaja rataa (Equatorial orbit).
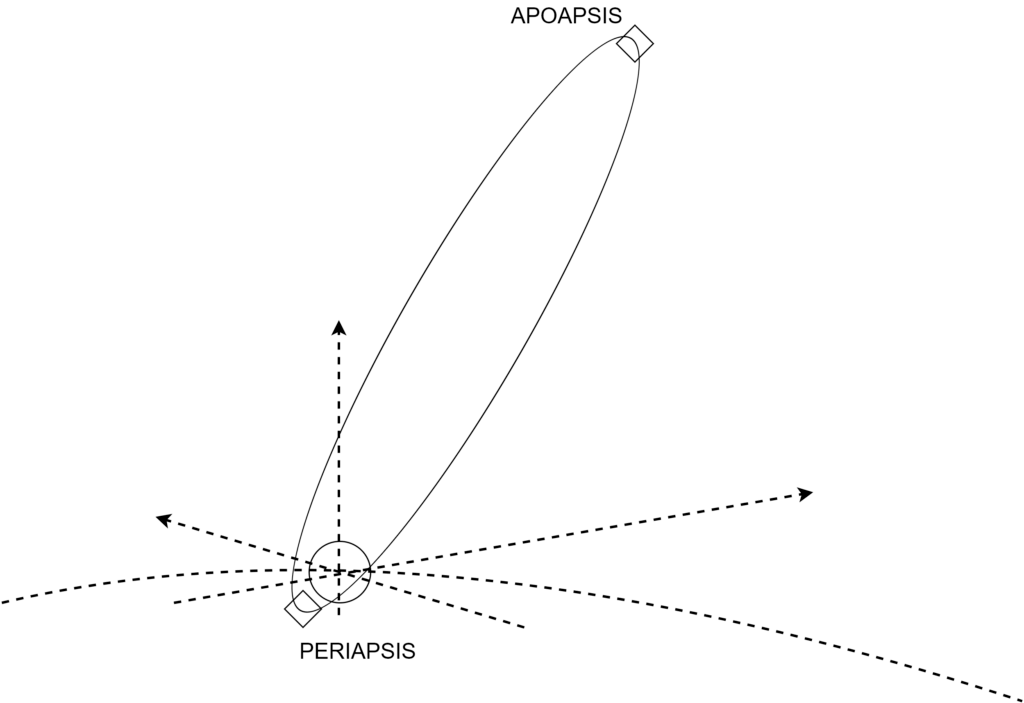
Kuva 2: Tasolla oleva ympyrärata
Tässä on nyt kaksi tärkeintä termiä. Periapsis ja Apoapsis; Tai koska olemme Maan kiertoradalla, Perigee ja Apogee. Perigee tarkoittaa radan alinta pistettä, ts. Pistettä jossa radalla oleva kohde on lähimpänä maapalloa. Apogee tarkoittaa pistettä jossa objekti on etäimmällään maapallosta.
Ympyräradan jakso on suhteellisen helppo laskea, kunhan radan eksentria (ellipsimäisyys) on riittävän matala. Ympyräradat joiden jakson pituus on yksi planetaarinen päivä, ovat äärimmäiset kiinnostavia ja arvokkaita satelliitti operaattoreille, jotka operoivat kommunikaatiosateliitteja.
Ellipsirata
Laajennetaan tätä rataa, mutta pysytään edelleen ratatasossa, mutta oletetaan, että satelliitti tekee polton jossakin kohdassa rataa, yleensä periapsiksessa. Poltto nostaa radan apogeeta ja tekee radasta elliptisen.
Asiat mutkistuvat pahasti kun rata on elliptinen, radan apoapsis ja periapsis ovat edelleen suhteessa radan massakeskipisteen kanssa, mutta toisin kuin ympyräradoilla, radan “keskipiste” ei sijaitse enää massakeskipisteessä vaan se on määritelty termillä isoakselin puolikas (eng semi-major axis), joka käsittää radan pituussuunnassa ja pikkuakselin puolikas, joka käsittää radan leveyssuunnassa, kun tarkkaillaan ratatasoa “yläpuolelta”.
Akselien nimikkeet eivät kuitenkaan ole syy miksi asiat mutkistuvat. Ratanopeus muuttuu nyt korkeuden funktiona- Ja tämä on jokseenkin vaikeaa kuvastaa sanoin; mutta mikäli ajattelemme, että objekti apoapsiksessa on hitaimmillaan ja alkaa tämän jälkeen putoamaan kohti periapsista kaarevalla radalla, se päätyy periapsikseen pudoten planeetan pinnan ohi ja saaden tarpeeksi energiaa voidakseen nousta uudelleen apoapsikseen, olemme jokseenkin ymmärtäneet miten ratanopeus käyttäytyy- Mitä korkeammalla radalla objekti on, sitä hitaammin se liikehtii, suhteessa pintaan.
Kallistuneet radat
Kolmiulotteisessa avaruudessa ratataso on pinta jossa katsomme objektien kiertävän. Jos rata ei ole ratatasolla, on radalla tällöin kallistumaa (inclination). Apogee ja perigee eivät ole sidoksissa ratakallistuksen suuntaan, vaan suhteessa kiertoratakeskustastaan olevaan korkeuteen.
Ja tässä kohdassa, juurikin tässä kohdassa orbitaali laskijat ilmeisesti huomasivat, että Kepler oli nero ja tämän asian käsittely onkin todella vaikeaa. Yllä olevaan kuvaan pitäisi nyt lisäillä periapsiksen ja aposiksen argumentit, merkitä radan kulkureferenssi ja nimetä kierorataobjetin kulmapoikkeama anomaliaksi, joka johtaisi kaikkia harhaan ja turmeltuisimme pahemman kerran.
Ollaan turmeltumatta ja, kuten kaikki amatööriastrofyysikot, siirrytään käyttämään NASAn HORIZONS sovellusta, johon pääsee käsiksi sivustolla: http://ssd.jpl.nasa.gov/horizons.cgi
| HORIZONS tarvitsee muutaman tiedon, jolla se osaa kertoa kaiken mitä olet koskaan halunnut tietää radoista.Mene sivustolle: http://ssd.jpl.nasa.gov/horizons.cgi Aseta kohtaan Observer @Sun; at merkki on osa syötettä.Kohdassa Table, valitse “Helio eclip. lon & lat”Tulosteesta löytyy kohta “hEcl-Lon” ja “hEcl-Lat” joka on asteissa, delta joka on astronomisina perusyksikköinä AU. |
Radan korkeus
Radan maapallon ympärillä voidaan jaotella niiden korkeuden mukaan (maapallon pinnasta, ei kiertoratapisteestä joka on maapallo/kuun orbitaalipiste. Palataan siihen toisella kertaa). Samalla paljastuu orbitaalimekaniikasta kiintoisa yksityiskohta. Mitä korkeammalla radalla sateliitti on, sitä matalampi on ratanopeus.
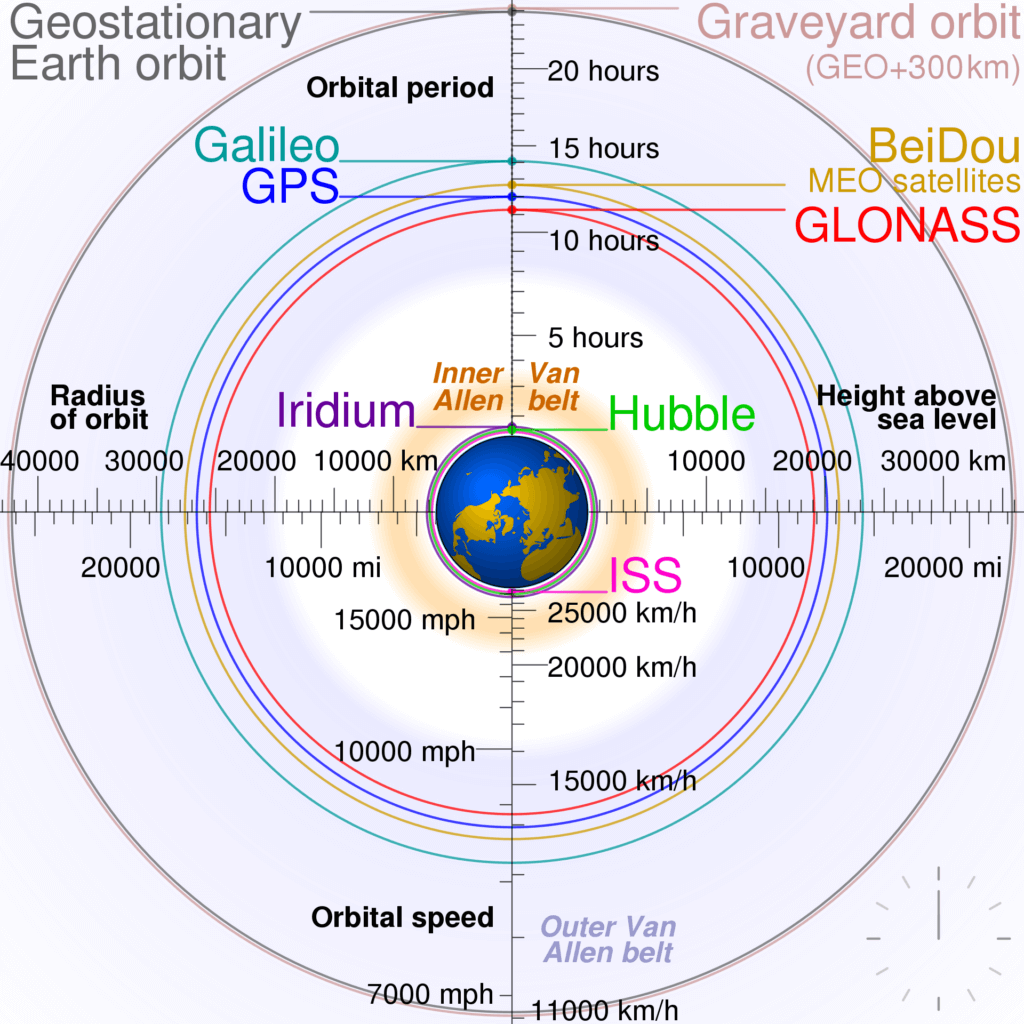
LEO
Low Earth Orbit: 160 km … 2000 km. Ratanopeus noin 8 km/s, joka antaa kiertoajaksi noin 90 minuuttia.
MEO
Medium Earth Orbit 2000 … 35,786 km; Ratataso jolla kierrätetään useita navigaatio, kommunikaatio ja tiedesateliitteja. Kiintoisasti ratakorkeus 20 200 km antaa orbitaali kiertoajaski 12 tuntia, joka tekee tästä radasta halutun GPS, GLONASS ja GALILEO sateliitti ohjelmille.
GEO
Geosynchronous equatorial orbit, tai geosynkroninen rata, on ympyrärata, päiväntasaajan päällä jonka kiertonopeus ja suunta on sama kuin maan kierto.
Tämän radan tärkein ilmenemä on geostaattinen rata, jolla tarkoitetaan kiertorataa, jonka kiertonopeus on sama kuin maan pinnan; toisin sanoen, sateliitti pysyy saman maapisteen päällä jossa sateliitti saavutti geostaattisen rada ja sai aikaiseksi ympyräradan. Sateliitti tällaisella radalla kykenee kommunikoimaan maa-aseman kanssa suoralla radiolinkillä.
HEO
High Earth Orbit; kiertorata joka on muodoltaan ellipsoidi ja jonka apogee on yli 35 786 km ja perigee alle 2 000 km; tämä rata tyyppi on hallitseva siirtymäradoissa ja sotilaallisissa sovelluksissa, joissa halutaan kahdella sateliitilla tehdä tiedustelua kohteesta.
Esimerkkeinä radan korkeuksista on wikimedia commonsissa julkaistu ratatataulu, josta käy ilmi sekä radan korkeus, käyttötarve, ratanopeus, että radan jakson pituus.
Erikoisradat
Edellä on mainittu tyypilliset radat ja niiden korkeudet- Rataparametrejä muuttamalla saavutetaan rata jolla kiertoradalla oleva satelliitti voi toteuttaa tehtävänsä.
Seuraaviin kappaleisiin on kerätty muutamia erityyppisiä ratoja, joita toteuttavat jotakin hyvin spesifiä tarkoitusta.
Polaariset Radat
Inklinaatio tarkoittaa radan kulma-eroa ratatasoon nähden; Jos tämä viedään absoluuttiseen ääripäähän, saadaan aikaiseksi polaarirata, jossa satelliitti kiertää napojen ylitse ja planeetta kiertää satelliitin alla.
Kuva 3: “Polaarirata”
Tämä rata on tarpeen kun halutaan tarkkailla yksittäisellä sateliitilla suurta joukkoa datapisteitä jotka sijaitseva laajalla aluella; Esimerkiksi jos halutaan ottaa vaikkapa Maasta koko planeetan laajuinen karttakuva.
Merkittävä polaarinen rata on nk. Aurinkosynkronen rata (Sun Synchronous orbit), joka on synkronoitu geolokaatioon suhteessa aurinkoon, toisin sanoen jos sateliitti ylittää keskipäivällä Helsingin, se ylittäisi helsingin joka päivä aina samalla aikahetkellä. Tämä antaa mahdollisuuden tarkkailla aika riippuvaisia muutoksia tarkkailtavalta maa-alueella.
Molnya
Erikoisradoista puhuttaessa Molnya-rataa ei voi ohittaa. Se on elliptinen polaarirata (inklinaatio >63 astetta), jolla saavutetaan puolen päivän ratajakso.
Molnya, tai “Salama” rata (“Молния”) on tarkoitettu korkean leveysasteen kommunikaatiosateliittien ratakäyttöön. Radalla on taipumus viettää suurin osa ajasta yhdellä puolella maapalloa ja kulkea nopeasti toisen puolen ohi. Suurin etu geostaattiseen rataan on jyrkempi kohtaamiskulma planeetan pintaan joka tekee kiertoratakuvauksesta tarkempaa. Geostaattinen rata ei kykene kohdentamaan samoille leveysasteille- Koska geostaattiselta radalta korkealla leveysasteella oleva kuvauskohde on likipitäen vaakatasossa.
Hautusmaaradat (Eng. Graveyard Orbits)
300 km geosynkronisen radan yläpuolella ovat hylkyradat tai hautausmaaradat, johon edelleen hylätään raketteja ja sateliitteja joiden käyttöikä tai operaatioikkuna on tullut päätökseen. Rata on noin 300km geosynkronisen radan yläpuolella. IADC määrittelee radan lisäkorkeudelle kertoimen ΔH= 235 = (100 Cr A ⁄ m) km
Jossa Cr on auringon säteilypaine ja A/m on satelliitin sivuleikkauksen ja massan suhde.
Miksi? Koska 300km orbitaalin nosto maksaa 11m/s ja perigeen pudottaminen ilmakehään maksaa tältä korolta 1,5km/s. 1500m/s delta-v kääntyy rahaksi, ja kaupalliset toimijat, niin pitkään kuin nämä radat ovat sallittuja,yritykset ja järjestöt dumppaavat niille romunsa.
Lagrange pisteet
Lagrangen pisteet ovat erikoistapaus orbitaalipisteistä kahden taivaankappaleen välillä. Ne ovat pisteitä avaruudessa jossa objektit yleensä pysyvät paikallaan. L1 tapauksessa Maan ja auringon vetovoimat kumoavat toisensa ja radan prekessio ei aiheuta haitallista rataeksymää. Lagrange pisteitä voidaan siten pitää kiertävän koordinaatiston ansiosta erikoistapauksena ympyräradasta.
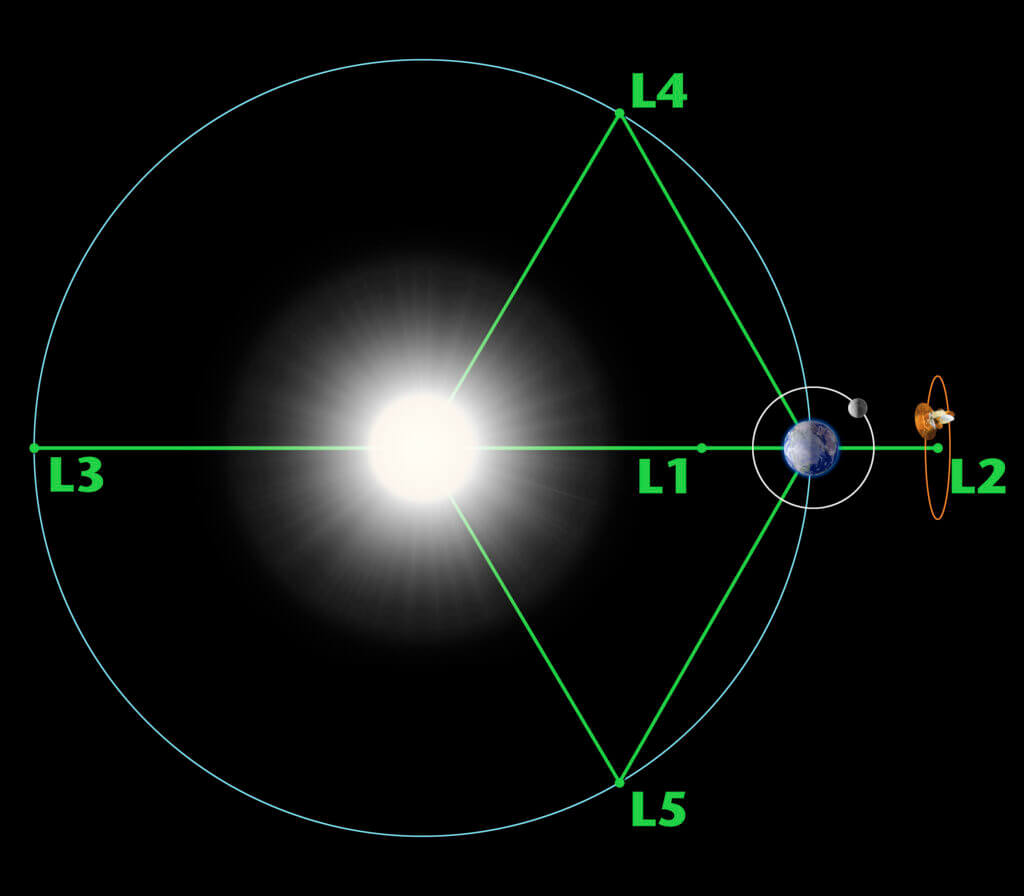
Lagrangen pisteitä voi ajatella matkustajalaivan autokantena. Ajaminen kannelle maksaa polttoainetta, mutta muutoin auto on vain rahtia; laiva tosin on painovoimapiste avaruudessa jota ajaa eteenpäin planetaarinen kiertoliike.
L1, L2 ovat “arvottomia” pisteitä, sillä näiden Lagrangen pisteiden sijainnit eivät ole riittävän vakaita tuomaan todellista lagrange rataa ja L3 on diametrisesti vastakkainen maan kanssa joten sen käyttöarvo on mitätön. L4 ja L5 sitä vastoin ovat usein esillä keskusteluissa, varsinkin kun keskustellaan siirtokunnista. Etenkin L4 on kiintoisa, sillä etäisyys Maa – Kuu on täsmälleen sama kuin L4 – Terra, ja Luna -L4. Tämä tarkoittaa, että L4 on samalla etäisyydellä Maasta kuin Kuu on maasta (384,400 km). Tämä tarkoittaa delta-v budjetin säästöjä.
Siirtymät
Siirtymät ovat kiertoratoja, joilla kirjaimellisesti siirrytään aurinkokunnassa kohteelta toiselle, mutta ne toimivat jokseenkin samalla tavoin kuin aikaisemmat radat. Niiden on tarkoitus tarjota lentorata yhden planeetan tai taivaankappaleen vaikutusalueelta toisen taivaankappaleen vaikutusalueelle.
Hohmann-siirtymä
Hohmann siirtymä edustaa delta-v budjetin minimointia halutulla radalla kahden taivaankappaleen välillä. Hohmann-siirtymä on yleensä pisin siirtymä-ajaltaan kahden kohteen välillä, mutta joitakin poikkeuksia on. Hohmann siirtymän heikkoutena on siirtymäradan muodostaminen ja radalta poistuminen
Siirtymäradan muodostus toimiii seuraavasti: Radan Apoapsiksen kohottaminen tapahtuu moottori impulssilla (tekemällä poltto) periapsiksssa radan kulkusuunnan suuntaisesti, (prograde). Jos poltto tehdään retrograde suuntaan (kulkusuuntaa vastaan), apoapsis putoaa. Tämä on tärkeä huomata kun kun tehdään radalta poistumaa.
Näin ollen, mikäli esimerkkiraketti haluaa lentää Maasta marsiin, on sen ensin tehtävä irroituspoltto maassa, jos ratalaskija on tehnyt työnsä hyvin, niin radan perigee osuu maan radan perihelionin kanssa kohdilleen ja raketti kuluttaa reaktiomassaa (delta-v), kohottaakseen rataansa marsin radan leikkaukseen.
Raketti jatkaisi radallaan, tehden vain Marsin ohilennon, mikäli raketti ei tekisi radan aphelionissa injektiopolttoa jolla raketti saapuisi marsin kiertoradalle. Marsin radalla raketti sitten voisi vakioda ratansa tekemällä retrograden suuntaan polton jolla periares (Marsin radan alin piste putoaa) ja toisen impulssin vakioidakseen rataansa tarkemmin, polttamalla jälleen retrograde suuntaan, mutta tällä kertaa Apoareksessa.
Bi-elliptic
Tupla-elliptinen rata edustaa kiintoisaa anomaliaa kiertoradoissa, jossa, lyhyesti hyödynnetään nk. Oberth-efektiä (radan nopeus lisää propellantin aikaansaamaa delta-v’tä). Jos halutaan korottaa rataa, tuplaellipsillä, alkuunsa rakatin on annettava impulssi radan pisteessä A ja korotettava radan apoapsis tasolle B, jota kuvaa keltainen ellipsi. Tämä on ensimmäinen siirtymäellipsi, jolla raketti kulkee kohti pistettä B.
Kun raketti saavuttaa pisteen B, se suorittaa uuden impulssin jossa radan periapsis nostetaan korkeuteen C- joka on toinen siirtymä ellipsi. Pisteessä C, joka on radan periapsis, tehdään radan pyöristys halutulle korkeudelle.
Ei liene yllättävää, että tupla-ellipsit eivät ole jokaisella siirtymällä budjetiltaan parempia kuin Hohmann-siirtymät, vaan ratojen säteiden suhteen ollessa 15,58 kertaa suurempia, ovat kaksois-elliptiset radat tehokkaampia delta-v budjetiltaan.
Jatkuvapolttoiset radat
Tai paremmin tunnettuna Brachistochrone siirtymäradat. Ajatuksena on tuottaa rakettimoottorilla impulssi koko matkan ajan. Tämä johtaa suunnattomiin delta-v tarpeisiin, eikä siten ole edes mahdollinen ilman hypoteettisia moottoreita tai eksoottisia propulsiolähteitä. Ainoat impulssit joissa edes sivutaan brachistochrone ratojen suuntauksia ovat pitkäkäyttöiset elektrostaattiset moottorit, kuten hall-effect moottorit ja ionimoottorit.
Delta-V Kartta
Tämä on kaikki kovin vaikea hahmottaa ilman jotakin kättä pidempää. Tietysti, “Fundamentals of Astrodynamics” antaa kokoelman kaavoja joilla lähestyä delta-v vaatimuksia jos haluaa laskea, mutta… on helpompi vain katsella taulukkoa tai karttaa.
Nk. Delta-v kartta antaa käsityksen millaisista delta-v budjeteista puhutaan kun liikutaan aurinkokunnassa. Toki, nämä ovat ideaalisia hohmann-siirtymiä (pienin mahdollinen delta-v), mutta ne antavat suuntaa.
Kuva 6 esittää delta-v karttaa lähiplaneetoista- Jokainen musta piste on rata, ja jokainen nuoli on poltto jolla radalle pääsee. Kartta ei tee eroa onko rata elliptinen, kuinka suuri radan kallistus on. Ja jos halutaan palata takaisin, samat askeleet pitää kulkea takaisin, jotta saadaan summittainen budjetti delta-v:lle.
Tämä on varsin epätarkka tapa laskea propellanttitarpeita, mutta kartta antaa oivallisen käsityksen siitä, kuinka korkeista delta-v budjeteista on puhe, kun lennetään lähiavaruudessa. Koko aurinkokunnan kartan löytää helposti hakukoneilla.
| Esimerkkejä raketeista ja niiden delta-v budjetista:Saturn-V, Apollo 11: 22 km/sAvaruussukkula 9.4 km/sSpaceX Falcon-9 (tehtävästä ja blokista riippuen) 9.8 km/s … 12 km/sAriane-V (tehtävästä riippuen): 9.7 km/s .. 11.5 km/sS-7 (blokista ja tehtävästä riippuen) ~10km/s – Ja lähtö on maapallolta… |
Loppusanat
Tämän artikkelin yhteydessä on nyt kerrottu huomattava joukko erilaisia kiertoratoja ja niiden sovelluksia. Mitä tästä olisi suotavaa muistaa? Lyhyesti, delta-v kartan luku, sillä se antaa hyvän käsityksen siitä mitä matkustaminen aurinkokunnan sisällä maksaa, oikeasti. Tsiolkovskin yhtälö kertoo suoraa miten monta tonnia propellanttia tämä sitten on.
Kenties myöhemmissä artikkeleissa voidaan keskustella mitä ovat Lissajou-, halo, geostaattiset siirtymäradat ja lukemattomat määrät kiertoratoja joita ei tässä artikkelissa nyt käyty läpi.

